Multirate Shading with Piecewise Interpolatory Approximation

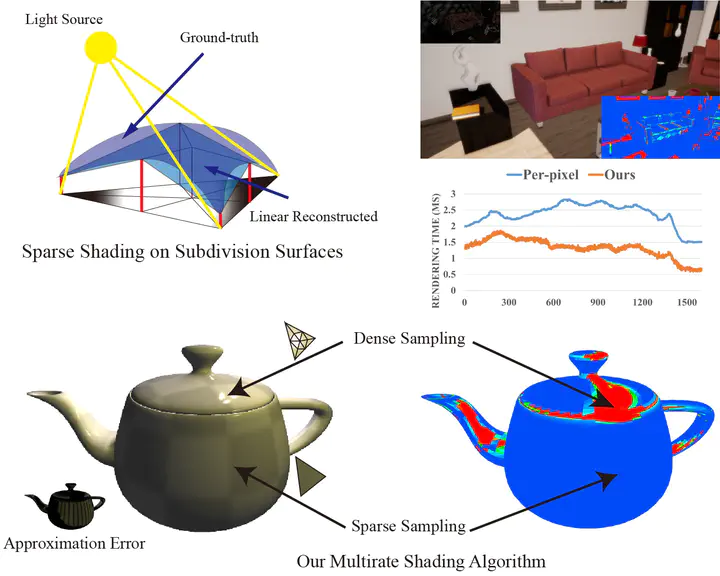
Abstract: Evaluating shading functions on geometry surfaces dominates the rendering computation. A high-quality but time-consuming estimate is usually achieved with a dense sampling rate for pixels or sub-pixels. In this paper, we leverage sparsely sampled points on vertices of dynamically-generated subdivision surfaces to approximate the ground-truth shading signal by piecewise linear reconstruction. To control the introduced interpolation error at runtime, we analytically derive an L-infinity error bound and compute the optimal subdivision surfaces based on a user-specified error threshold. We apply our analysis on multiple shading functions including Lambertian, Blinn-Phong, Microfacet BRDF and also extend it to handle textures, yielding easy-to-compute formulas. To validate our derivation, we design a forward multirate shading algorithm powered by hardware tessellator that moves shading computation at pixels to the vertices of subdivision triangles on the fly. We show our approach significantly reduces the sampling rates on various test cases, reaching a speedup ratio of 134%~283% compared to dense per-pixel shading in current graphics hardware

Video: